プレスリリース 汎化能力を最大化する特徴抽出―信頼性・説明可能性の高いデータ予測―
プレスリリース
理化学研究所
日本医療研究開発機構
理化学研究所(理研)脳神経科学研究センター脳型知能理論研究ユニットの磯村拓哉ユニットリーダーと数理脳科学研究チームの豊泉太郎チームリーダーの研究チームは、将来の入力を予測するために最も有益な成分を抽出する教師なし学習[1]手法「PredPCA(予測主成分分析)」を開発しました。
本研究成果は、自動運転や医療診断など、解の一意性や精度保証が重要な状況における予測の信頼性の保証に役立つと期待できます。
未経験のテストデータに対して学習結果を一般化することを「汎化」といいます。時系列予測の汎化は、人工知能や脳科学における重要な課題です。しかしこれまでの手法では、汎化性能が悪いことや最適でない解に陥ってしまうといった問題がありました。
今回、研究チームは、予測不可能なノイズを効率的に除去しつつ、解が一意に定まるような最適化方法によって、テスト予測誤差を最小化する手法を数理的に導きました。PredPCAを用いると、訓練データ数と入力次元が十分大きい場合に、入力信号を生成する外部システムの隠れた状態変数やパラメータを高い精度で同定できます。例えば、動画から予測の汎化に重要な隠れた特徴を抽出することが可能です。
本研究は、科学雑誌『Nature Machine Intelligence』オンライン版(令和3年4月12日付:日本時間令和3年4月13日)に掲載されます。
- 研究支援
- 本研究は、日本医療研究開発機構(AMED)「革新的技術による脳機能ネットワークの全容解明プロジェクト(領域代表者:宮脇敦史、岡野栄之)」、日本学術振興会(JSPS)科学研究費補助金新学術領域研究(研究領域提案型)「マルチスケール精神病態の構成的理解(領域代表者:林(高木)朗子)」による支援を受けて行われました。
背景
「予測」は生物や人工知能にとって不可欠な能力です。特に実世界では、限られた数の過去の経験(訓練データ)から学んだ知識のみに基づいて、新たに遭遇した入力信号(テストデータ)のダイナミクスを予測する必要があります。このように、以前に見たことのない入力データの将来の結果を予測する能力を「汎化」といいます。汎化能力は、訓練予測誤差とテスト予測誤差の差である「汎化誤差」で決まるため、汎化誤差の小さい予測手法を見つけることが重要です。
機械学習[2]や統計の分野では、これまでさまざまな予測手法が報告されてきましたが、現在主流の機械学習アプローチにはいくつかの限界があります。それらのアプローチと問題点は、大きく次の三つに分けられます。
- 予測モデルの中で古くから使われ、最も単純なのは自己回帰モデル[3]です。しかし、自己回帰モデルは冗長性が高いため、訓練データのゆらぎに引きずられて過学習[4]を起こしやすく、汎化誤差が大きくなってしまいます。そのため、良い情報表現を得るには次元削減[5]を行う必要があります。
- 最も広く使われている次元削減・特徴抽出の手法は、主成分分析(PCA)[6]です。しかし、PCAは予測に関係のないノイズを多く抽出してしまうため、汎化能力の最大化とは必ずしも相性が良くありません。
- 現在、予測に広く使われている手法は状態空間モデル[7]です。これは、入力信号を生成した非線形生成過程[8]の隠れた状態変数とパラメータを推論する手法です。しかし状態空間モデルは、背後のダイナミクスが未知の場合に最適でない解(局所最小値)に陥ることがあり、生成過程を正しく推論できない点が問題です。
このように従来のアプローチは、汎化誤差が大きいか、局所最小値を持つことが知られており、どちらも未経験のテストデータを予測する際の誤差が大きくなります。そこで、研究チームは、自己回帰モデルとPCAの良い点を組み合わせた新しい教師なし学習手法の開発を目指しました。
研究手法と成果
今回研究チームは、将来の入力を予測するために最も有益な成分を抽出する教師なし学習手法を予測誤差最小化の観点から数理的に導き、「PredPCA(予測主成分分析Predictive Principal Component Analysisの略)」と名付けました(図1)。PredPCAは、予測を担う部分(図1の青)と次元削減を担う部分(図1の緑)から構成され、両者を同時に最適化する解を解析的に求めることができます。この構成により、予測不可能なノイズを効率的に除去しつつ、解が一意に定まるような最適化方法(凸最適化)によって、テスト予測誤差を最小化できます。
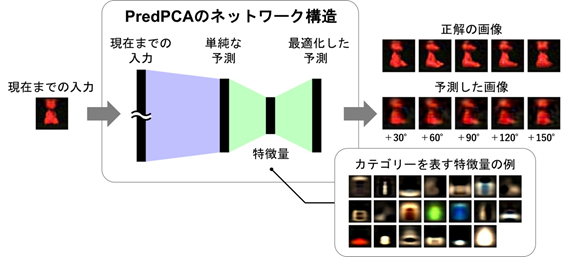
さらに、数理解析により、十分な訓練サンプルと十分に高次元な入力があれば、PredPCAは標準的な非線形生成過程の隠れた状態変数、パラメータ、次元を高い精度で同定できることを示しました。凸最適化のため、従来の状態空間モデルとは異なり、同定されたシステムの特徴は与えられた訓練データに対して一意に決まるのが利点です。これらの優れた特性は、研究チームが過去に証明した漸近線形化定理[9]の帰結として導かれました注2)。本研究は「十分な訓練サンプルと高次元入力があれば、ノイズを含む入力信号のみに基づいた教師なし学習によって、標準的な非線形生成過程をシステム同定[10]できる」ことを理論的に保証した初めての研究です。
次に、自然動画を用いてPredPCAの汎化予測と特徴抽出の性能を評価しました。一つの例では、反時計回りに回転している3次元物体の画像を入力として、ニューラルネットワーク[11]を訓練しました。そして、(訓練データセットには含まれない)テストデータセットの物体の半分の面(-180°から±0°の画像)だけを観察し、反対側の面(±0°から+180°の画像)を予測する課題を行いました。その結果、PredPCAは以前に見たことのないテストデータの物体が+30°、+60°、+90°、+120°、+150°回転した姿を予測できました。図2は、+90°回転した画像の予測結果を表しています。

一般に、テスト予測誤差は訓練サンプル数の増加に伴い減少していきます。理論予想通りに、PredPCAのテスト予測誤差は、自己回帰モデルよりも早期に減少していきました。また、テスト予測誤差の平均値を状態空間モデルなどの従来手法よりも小さくすることができました。
加えて、PredPCAが抽出した成分に対して、さらにPCAと独立成分分析(ICA)[12]を適用したところ、得られた低次元の特徴量の各次元が色や形状などの物体のカテゴリーや3次元空間内での角度といった予測に重要かつ直感的に意味の分かる情報を表していることを確認しました(図1の下部パネル参照)。従来手法とは異なり、教師なし学習と凸最適化という条件の下でこれらの特徴抽出ができたことは特筆に値します。
これらの結果は、PredPCAが限られた訓練データのみを用いて、一般的な物体が回転する際の画像変化の法則を同定できたことを示唆しています。なお、元画像の輝度の分散と同程度の分散を持つ大きなホワイトノイズ[13]を人為的に画像に追加した場合でも、PredPCAはこれらの汎化予測と特徴抽出の結果を維持することができました。このことから、(理論予想の通りに)PredPCAが観測ノイズに対して高いロバスト性[14]を持つことが示されました。
注1)Geusebroek, J. M., Burghouts, G. J. & Smeulders, A. W. The Amsterdam library of object images. Int. J. Comput. Vis. 61, 103-112 (2005). (Dataset at http://aloi.science.uva.nl)
注2)Isomura, T. & Toyoizumi, T. On the achievability of blind source separation for high-dimensional nonlinear source mixtures. Neural Computation. In press. (Preprint at https://arxiv.org/abs/1808.00668)
今後の期待
PredPCAは、広い範囲の実世界データの汎化予測や特徴抽出に利用できます。前述の3次元回転物体データ以外にも、手書き数字の時系列や車の運転中に見える風景の動画データに対して、PredPCAを適用し性能を実証しました。風景動画の例では、未経験動画の0.5秒後を一定の精度で予測し、横方向の移動速度など予測に重要な情報を抽出することができました。PredPCAによる精度保証付きの汎化予測やシステム同定は、特に自動運転や医療診断のように、特徴抽出の失敗やシステムの誤認識や過学習によって、その後のアプリケーションに壊滅的な問題を引き起こす状況下で、信頼性の高い予測を行うために重要です。
本研究では自己回帰に焦点を当てましたが、PredPCAの枠組み自体は任意の関数の回帰問題における汎化誤差の最小化に利用できることから、さまざまな実世界アプリケーションが考えられます。特に、PredPCAはニューラルネットワークによる構成が簡単で計算コストが低いため、ニューロモルフィックデバイス[15]による大規模並列実装に適しています。数学的に保証された最適な汎化戦略として、PredPCAは、脳が行う汎化のメカニズムの解明や、信頼性の高い説明可能な人工知能(explainable AI)の開発への応用が期待できます。
論文情報
- タイトル
- Dimensionality reduction to maximize prediction generalization capability
- 著者名
- Takuya Isomura & Taro Toyoizumi
- 雑誌
- Nature Machine Intelligence
- DOI
- 10.1038/s42256-021-00306-1
- ソースコード
- https://github.com/takuyaisomura/predpca
補足説明
- [1] 教師なし学習
- ラベルや教師信号を使わずに学習する方法。主成分分析(PCA)や独立成分分析(ICA)が代表的。
- [2] 機械学習
- コンピュータが経験に基づき自律的に学習する方法。あるいはそれを研究する学問領域。
- [3] 自己回帰モデル
- Auto-regressive(AR)モデルともいう。現在までの入力信号を用いて、将来の入力信号を予測する手法。
- [4] 過学習
- 訓練予測誤差は小さいが、テスト予測誤差は大きい状態。訓練データのゆらぎに過剰に適合しようとするために起きる。予測手法の冗長性が大きいと過学習が起きやすい。
- [5] 次元削減
- 特徴抽出の標準的な方法。入力信号の次元を小さくする過程で、不必要な情報を削ぎ落とし重要な情報のみを抽出する。
- [6] 主成分分析(PCA)
- 多次元の入力信号の特徴を最も良く表す低次元の変数(特徴量)を見つけるための手法。特徴量から入力信号を再構成したときの損失を最小化するように特徴量を決める。PCAをディープラーニングに拡張したものは自己符号化器(オートエンコーダ)と呼ばれ、近年広く使われている。PCAはPrincipal component analysisの略。
- [7] 状態空間モデル
- 入力信号のみからその背後にある生成過程を推論する手法の総称。将来の入力信号や隠れた状態変数の予測に使われる。カルマンフィルタなどが状態空間モデルの一例である。一般的な問題設定では、隠れた状態変数、パラメータ、次元の全てが未知であるため正しくシステム同定することは困難であった。
- [8] 非線形生成過程
- 隠れた状態変数からどのように入力信号が生成されるのかをメカニカルに表す数式のこと。隠れた状態変数のダイナミクスを決める非線形写像と、隠れた状態変数から入力信号への変換を決める非線形写像によって特徴付けられる。それぞれの写像は、ホワイトノイズによるゆらぎを受けている。
- [9] 漸近線形化定理
- 訓練サンプル数が十分であるとき、隠れた状態変数の次元が十分大きくかつ入力信号の次元がそれよりさらに十分大きいという条件の下では、よく知られるPCAとICAの組み合わせによって、非線形生成過程の隠れた状態変数を高い精度で推論できることを数理的に示した定理。
- [10] システム同定
- 生成過程の隠れた状態変数、パラメータ、および次元を決定すること。
- [11] ニューラルネットワーク
- 脳の神経回路を模擬した計算方式。複数の単純な計算素子(ニューロン)が結合した回路を用いて並列に計算を行う。
- [12] 独立成分分析(ICA)
- 混ざり合った複数の入力(例えば複数のマイクで観測した音声信号)から、その背後にある個々の信号源を取り出すためのブラインド信号源分離の代表的な手法。潜水艦のソナー解析、ビデオ動画使った生体信号検出など、さまざまな分野で応用されている。ICAはIndependent component analysisの略。
詳しくは過去のプレスリリース(並列計算で感覚情報を分解(理化学研究所))を参照。 - [13] ホワイトノイズ
- ある時刻と別時刻の値の間に相関(自己相関)がない不規則なノイズのこと。
- [14] ロバスト性
- 頑強性、頑健性ともいう。外部環境の変化の影響を受けにくい性質のこと。
- [15] ニューロモルフィックデバイス
- 脳の回路を模擬したニューラルネットワークによって計算を実行する装置。並列処理能力や電力消費の面で既存のフォン・ノイマン方式の計算機より優れているとされる。
発表者・機関窓口
発表者
理化学研究所 脳神経科学研究センター
脳型知能理論研究ユニット
ユニットリーダー 磯村 拓哉(いそむら たくや)
数理脳科学研究チーム
チームリーダー 豊泉 太郎(とよいずみ たろう)
機関窓口
理化学研究所 広報室 報道担当
E-mail:ex-press[at]riken.jp
*今般の新型コロナウイルス感染症対策として、理化学研究所では在宅勤務を実施しておりますので、メールにてお問い合わせ願います。
AMED事業に関するお問い合わせ先
日本医療研究開発機構(AMED)疾患基礎研究事業部疾患基礎研究課
TEL:03-6870-2286 FAX:03-6870-2243
E-mail:brain-m[at]amed.go.jp
※上記の[at]は@に置き換えてください。
掲載日 令和3年4月13日
最終更新日 令和3年4月13日


